9.SciPy切比雪夫多项式
俄国著名数学家Чебышёв切比雪夫,是彼得堡数学学派的奠基人和领袖。
9.1 切比雪夫多项式递归公式
源起于多倍角的余弦函数和正弦函数的展开式,是与棣美弗定理有关、以递归方式定义的多项式序列,是计算数学中的一类特殊函数,对于注入连续函数逼近问题,阻抗变换问题等等的数学、物理学、技术科学中的近似计算有着非常重要的作用。 切比雪夫多项式在逼近理论中有重要的应用。这是因为第一类切比雪夫多项式的根(被称为切比雪夫节点)可以用于多项式插值。相应的插值多项式能最大限度地降低龙格现象,并且提供多项式在连续函数的最佳一致逼近。 $$T_0(x) = 1$$ $$T_1(x) = \cos\theta = x$$ $$T_2(x) = \cos2\theta$$ $$T_3(x) = \cos3\theta$$ $$\vdots$$ $$T_n(x) = \cos n\theta$$ 由于有: $$\cos n\theta = 2cos\theta\cos n\theta - cos(n-1)\theta$$ 故可得递推公式: $$T_{n+1}(x) = 2xT_n(x) - T_{n-1}(x) $$ 故而有: $$T_0(x) = 1$$ $$T_1(x) = x$$ $$T_2(x) = 2x^2-1$$ $$T_3(x) = 4x^3 -3x$$ $$T_4(x) = 8x^4-8x^2 + 1$$ $$\vdots$$ 由此可推得切比雪夫的重要性质:(1)$x^n$的系数是$2^{n-1}$; (2)只有偶(奇)次项只含有偶(奇)次方;(3)递推公式为:$T_{n+1}(x) = 2xT_n(x) - T_{n-1}(x) $
9.2 切比雪夫多项式零点
$T_n(x)$在$[-1, 1]$区间有n个不同的零点。 $$\cos\theta =x \Longrightarrow \theta = \arccos x $$ $$T_n(x) = \cos n\theta = \cos (n \arccos x)$$ 取$$ n \arccos x=\frac{(2k + 1)\pi}{2}$$ $$ \Longrightarrow \arccos x=\frac{(2k + 1)\pi}{2n}, k \in(0,1,\dots,n-1) $$则有 $$ x_k = \cos(\frac{(2k + 1)\pi}{2n}), k \in(0,1,\dots,n-1) $$ 由可知切比雪夫$T_n(x)$的n个零点全部在$[-1,1]$之间,且$T_n(x)$绝对值最大值为1。
9.3 N阶多项式展开
一个N次的多项式按切比雪夫多项式可展开为如下的形式:
$$p(x) = \sum_{n = 0}^{N} a_nT_n$$
还是以四个点坐标(1,1),(2,3),(3,5),(4,4)为输入数据来获得切比雪夫多项式展开。
由于有4个点,故x最高次数为3次方,所以$$p(x) = \sum_{n = 0}^{3} a_nT_n =
a_0 T_0(x)+a_1 T_1(x)+a_2 T_2(x)+a_3 T_3(x)$$
分别将以上四个点的$x_i$和$y_i$代入方程得:
$$p(1)=a_0 T_0(1)+a_1 T_1(1)+a_2 T_2(1)+a_3 T_3(1)
=1$$
$$p(2)=a_0 T_0(2)+a_1 T_1(2)+a_2 T_2(2)+a_3 T_3(2)
=3$$
$$p(3)=a_0 T_0(3)+a_1 T_1(3)+a_2 T_2(3)+a_3 T_3(3)
=5$$
$$p(4)=a_0 T_0(4)+a_1 T_1(4)+a_2 T_2(4)+a_3 T_3(4)
=4$$
这里有(见递推公式)
$$T_0(1) = T_0(2) = T_0(3) = T_0(4) = 1$$
$$T_1(1) = 1 , T_1(2) = 2, T_1(3) = 3, T_1(4) = 4$$
$$T_2(1) = 1 , T_2(2) = 7, T_2(3) = 17, T_2(4) =31$$
$$T_3(1) = 1 , T_3(2) = 26, T_3(3) = 99, T_3(4) =244$$
上边的p(1)~p(4)式子变为:
$$p(1)=a_0 +1\times a_1 +1\times a_2 +1\times a_3
=1$$
$$p(2)=a_0 +2\times a_1+7\times a_2 +26\times a_3
=3$$
$$p(3)=a_0 +3\times a_1+17 \times a_2+99\times a_3
=5$$
$$p(4)=a_0 +4\times a_1+31\times a_2+244\times a_3
=4$$
写成$Ax = y$矩阵的方式:
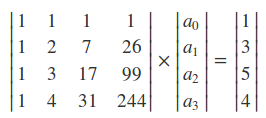
有了A和y便可求x(系数)了,A计算是手算的,Numpy库里numpy.polynomial.chebyshev模块提供了chebvander函数可以自动完成上述计算过程,称虚范德蒙矩阵。按上述思路程序设计如下:
import numpy.polynomial.chebyshev as chebyshev
import numpy as np
import numpy.linalg as linalg
x = np.array([1, 2, 3, 4])
y = np.array([1, 3, 5, 4])
deg = len(x) - 1
A = chebyshev.chebvander(x, deg)
print A, "# A"
c = linalg.solve(A, y)
print c,"# c"
for v in x:
print v, np.polynomial.Chebyshev(c)(v),"#p(%d)" % v
程序执行结果如下:
[[ 1. 1. 1. 1.]
[ 1. 2. 7. 26.]
[ 1. 3. 17. 99.]
[ 1. 4. 31. 244.]] # A
[ 3.5 -3.875 1.5 -0.125] # c
1 1.0 #p(1)
2 3.0 #p(2)
3 5.0 #p(3)
4 4.0 #p(4)
c的输出结果便是$$p(x) = \sum_{n = 0}^{N} a_nT_n$$ 切比雪夫多项展开式里的$a_n$即系数。
从c的输出结果$c[3] = -0.125$,即$T_3(x) $的系数$a_3 = -0.125 \times 2^{3-1} = -0.5$ 和范德蒙求解多项式 一节求得的$f(x) =2-3.5 x + 3x^2 -0.5 x^3$的三次项的系数是一致的。
而x的1次项系数应该是$T_1(x)$和$T_3(x)$相关即$a_1=-3.875 \times 1 + (-0.125) \times (-3) = -3.5 $也和范德蒙求解多项式 一节求得的$f(x) =2-3.5 x + 3x^2 -0.5 x^3$的一次项的系数是一致的。